| THE
GOING RATE.
Have you ever driven a street rod with suspension
that was too hard, or raced a car that refused to launch?
Chances are that, somewhere along the line, you might have
chosen the wrong rate springs...
|
|
In the not-so-distant past, it was considered
cool in the street rod world to visit your local breaker’s
yard, hunt out an old Jaguar Mk10 - or maybe even an E-Type
- and cut out the rear suspension assembly. Once home, the
unit would be stripped down, cleaned, chromed and detailed.
Next, it was bolted in place under the back end of a glass
fibre rod.
Seductive
The end result looked neat at a time when the alternative
appeared to be an Austin Westminster axle painted bright
red. Those chromed half-shafts twinkled seductively in the
evening light, the home-made bottom tie link proudly displayed
the legend ‘Ford’. Everything seemed perfect
- except for that mouthful of loose fillings on every journey.
See, nobody told you about spring rates.The complexities
of suspension and spring rates is not something you would
find explained in any street or hot rod resource guide.
In many ways, however, the Jaguar suspension
set-up was too seductive. Mounted on its own sub-frame,
all the budding rodder had to do was remove it from one
car and bolt it on to another, coilover shocks and all.
The problem was that the spring rates - the stiffness, if
you like - had been chosen with a car weighing a ton and
a half in mind, whereas the average street rod weighed about
half that. This resulted in a teeth-jarring ride that took
the fun out of any journey. Some rodders soon realised that
the ride quality could be dramatically improved by the simple
expedient of removing one shock from each side (the Jag
IRS system has four coilovers in all),
although on a heavier car that would often make the ride
too soft. However, it was a step in the right direction.
Fast-forwarding to the present day, by and large the Jaguar
IRS has fallen out of fashion in favour of home-brewed independent
set-ups or, more commonly, four-link mounted live axles.
In drag racing circles, the four-link, or ladder bar, reigns
supreme.
If you drive a car that retains its factory suspension,
then rarely is there much cause to make radical changes
to the spring rates. Only when you start putting massive
amounts of horsepower, or removing a whole load of weight,
does the matter of spring rate start to rear its head. On
a race car, weight transfer is heavily affected by spring
rates, so careful consideration must be given.
|
|
 |
|
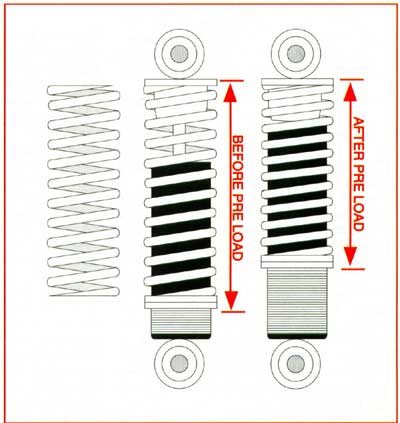 |
Above:
When a spring is put under load by the vehicle weight,the difference
in length from the maximum extension to length at ride height
is the 'rebound' height. |
|
|
Above:
If a softer spring is fitted, the ride height is restored
by pre-loading the spring. This is done by winding up the
bottom cup. Softer springs can allow a race
car to react more quickly. This is NOT
recommended for street use!!! |
|
Spring
Rate
If however you throw away the factory suspension and hang
the rear axle on a four-link or ladder bar assembly, then
you must calculate what rate springs
you need. OK, so you can guess - or copy what someone else
has done - but, to get things right for your car, it’s
worth spending a little time doing some basic mathematics.
The end result will be worth it.
The stiffness - or rate -
of any spring is measured in lbs/in. As this suggests. it
is the measure of the amount of load in pounds necessary to
compress the spring by un. For example, a 200lbs/in spring
will compress by 2ins if a load of 400lbs is exerted on it.
The first thing to do - and here we will talk largely about
four-bar or ladder bar installations
- is to establish what length shock you will need. This will
frequently be governed by space restrictions but, as a general
rule, coilover units such as those in the Koni SPA-1 range
(the drag racer’s favourite) are available in fully-extended
lengths, measured eye-to-eye, ranging from 15/ins to 19/ins.
An important measurement is the stroke - that’s the
difference in length of the shock from full extension to full
compression. This doesn’t vary as much as the fully
extended length - something between 5ins and 7ins being the
norm.
In our hypothetical installation, we’ll take it that
the car needs a shock which is approximately 16ins long. Now,
one thing to make clear at an early stage is that a shock
is best mounted at a tangent to the arc of movement of the
suspension components.
In a ladder bar situation, this is easy to establish as the
suspension pivots about the front mounting point of the ladder
bar. In a four-bar installation, the suspension pivots about
the Instant Centre - that’s the imaginary intersection
point of the upper and lower four-bar links.
Corner Weights
To work out what rate springs we need, we must establish the
true corner weights of the car. The corner weight is literally
the weight of the car as measured at each wheel. Add all four
corner weights together and you get the total weight of the
vehicle.
Note, however, that we said ‘true’ corner weights.
What we need to throw out of the equation is the ‘unsprung
weight’ - that’s the weight of all the suspension
components that actually move. This will include the wheels,
tyres, hubs, bearings, brakes and a proportion of the suspension
links (wishbones, four-bar etc). The true corner weight is,
therefore, the total corner weight minus the unsprung weight.
With the chosen shock unit bolted in place, you need to measure
the available travel. This is not the same as the full travel
of the shock from fully open to fully compressed, but the
travel from fully extended to the chosen ride height. On a
shock with 7ins of available travel, this should normally
be about 5ins, leaving 2ins for ‘bump’ travel
(that is, upwards movement of the suspension components.
To establish a ballpark spring rate for our hypothetical installation,
let us say that the corner weight is 1,080lbs. If the unsprung
weight measures up to 80lbs, the true corner weight will be
1,080 -80 = 1,000lbs. Divide this by the 5ins of travel (1000÷5)
and the result is 200lbs/in.
You could replace that spring with a softer one - say 150lbs/in
- but then the suspension would settle more, reducing the
ride height. In our first example, shock travel from full
extension to ride height is: corner weight÷spring rate
(ie 1,000÷200) = 5ins. In our second example, this
would be 1000÷150 = 6.66ins, meaning that the car will
sit 1.66ins (6.66 - 5) lower than we want. To re-establish
the correct ride height, we must pre-load the spring by moving
the lower adjustable spring cup up by 1 .66ins.
The advantage of using a softer rate spring is that the suspension
will react more quickly and in a drag race application, that
could be just what you want - especially in a heavy Super
Stock type of vehicle where rapid weight transfer is necessary.
However, you must be aware that, whereas with a 200lbs/in
spring, it will take a load of 400lbs to compress our’
shock that final 2ins of bump travel, whereas with a 150lbs/in
spring this figure will drop to just 300lbs.
|
|
|
|
|
 |
 |
| Left:
The Motion Ratio is calculated by dividing the distance from
the suspension pivot point to the bottom spring mount (A)
by the distance from the pivot point to the tyre contact patch
(B). This is true for both A arm and strut suspension systems.
Above: If spring is not mounted on a tangent,
calculate spring rate after measuring vertical distance between
pivot and top of spring (C), and length of spring at ride
height (D).
|
|
|
|
|
| Ideal
World
In an ideal situation, a softer spring
will always benefit reaction and 60ft times. It will also
help the vehicle to cope better with an undulating track -
and we've all raced on one of those at some time!
However, the disadvantage is that spring life will be reduced
(ie the spring will settle) and this can be detected by a
change in ride height. Softer springs are also more prone
to coil bind -the condition where the coils of the spring
are forced into contact with each other.
On any suspension set-up, the bottom mount of the coilover
- and here we must include strut type front suspension systems
- will not be directly over the centreline of the wheel and
tyre.
Almost without exception, the mounting point will be inboard
of the centreline. What we need to calculate is the Motion
Ratio.
To do this, it is necessary to measure the distance from the
pivot point of the suspension to the bottom mount of the coilover
(length ‘A’) and from the pivot point to the centre
of the contact patch of the tyre (length ‘B’).
The Motion Ratio is calculated as A÷B.
From this we can now calculate the true spring rate required
which is:
True Corner Weight x Motion Ratio
0000000 Available Travel
This same equation
can be used to accurately work out the required spring rate
of a four-bar system as long as you remember that the length
‘A’ will be measured from the Instant Centre (IC)
to the lower shock mount and length ‘B’ will be
measured from the IC to the centreline of the rear axle.
Calculations
If for any reason the shocks are not mounted at a tangent
to the arc of suspension movement, then we can still calculate
the required spring rate, although things do get a little
more complicated. Here we need to make another measurement:
the vertical (or ‘actual’) distance between
the upper shock mount and the pivot point of the suspension
system - distance ‘C’.
To calculate the required spring rate, we must now use the
following formula:
Corner Weight x Spring Length x Motion Ratio
0000Available Travel x Vertical
Distance
Let’s put some figures to this:
True Corner Weight = 1,000Ibs
Length of Coilover = 15ins
Available Travel = 5ins
Vertical Distance = l2ins
Motion Ratio = 0.75
Spring Rate = 1,000 x l0x 0.75 = 187.5lb/in
..........................5 x
12
We can see that if such factors as Motion Ratio are ignored
then we would get a different answer altogether:
Spring Rate 1,000 x 15 = 2501bs/in
........................5x 12
The final consideration when
choosing springs is to ensure that the front and rear spring
frequencies are different. If they were exactly the same,
every time a car hit a bump, it would want to ‘porpoise’.
Most of you will have at some time seen a drag race car bucking
and heaving back and forth off the line - this is often the
result of having ill-matched springs front and rear. By ensuring
that one spring does not compliment the other, you can make
certain that this porpoising is eradicated.
You cannot so readily calculate
the frequency of a spring, but you can read it from the graph!
The frequency is expressed in cycles per minute (CPM).
Hopefully this will have given you an insight into how to
work out what rate springs you need to give your car a fighting
chance on the street or strip.
|
Below:
If a car has front and rear springs of the
same frequency, the result is ‘porpoising’- a
tendency to buck back and forth. If you know the corner weight,
you can read off the spring frequency - measured in cycles
per minute (CPM) - from the, graph below. What you need to
calculate is the Wheel Rate (a measure of the actual force
and travel seen at the wheel):
Wheel Rate = Spring Rate x (Motion Ratio)²
Front and rear spring frequencies must differ. |
|
 |
|
|
|
|
|




